Boletín Mamut Matemáticas, enero 2015 |
|
¡Hola!
En este boletín exploramos la sucesión Fibonacci y la razon áurea, más tengo hojas de ejercicios para graficar rectas y ecuaciones lineales, esta vez en los dos formatos html y PDF. 1. La sucesión Fibonacci y la razon áurea (grados 7-12) 2. Ejercicios para graficar rectas (grados 7-9) |
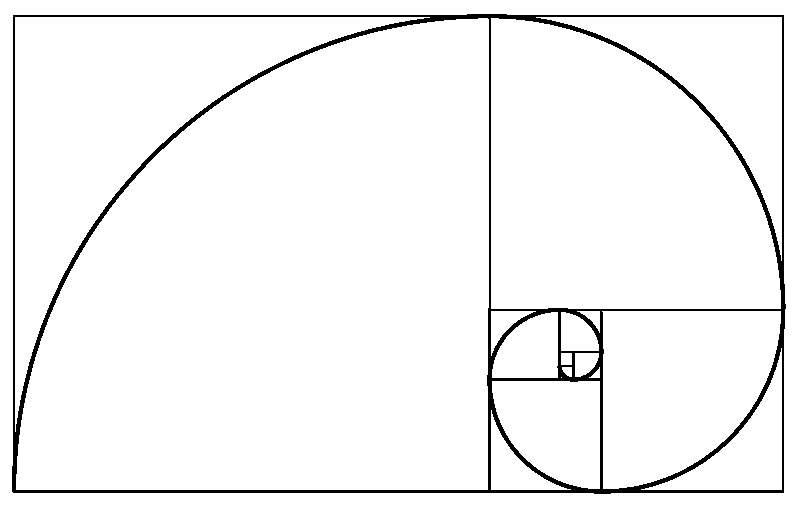
1. La sucesión Fibonacci y la razon áureaEsta lección es sobre la secuencia de Fibonacci y la razón áurea, apta tanto para la escuela media (primera parte) como para los estudiantes de matemáticas de secundaria (bachillerato). Pregunta a tus alumnos, cómo creen ellos que sigue esta secuencia de números: 0, 1, 1, 2, 3, 5, 8, 13, 21... La solución es la siguiente: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... Sencillamente tienes que sumar dos números consecutivos de la secuencia para obtener el siguiente. Por ejemplo, 0 + 1 = 1. Luego, 1 + 1 = 2. Luego, 1 + 2 = 3. Y así sucesivamente. Esta secuencia se llama secesión de Fibonacci o números de Fibonacci. Y no es simplemente cualquier secuencia: tiene algunas propiedades increíbles, y además aparece en la naturaleza en muchos lugares. Por ejemplo, puedes revestir un piso con baldosas cuadradas cuyos lados son números de Fibonacci consecutivos: 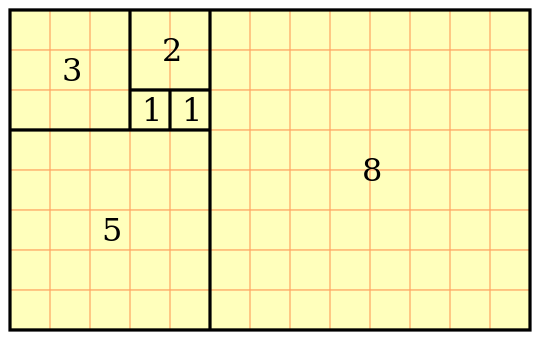 Un piso con baldosas cuadradas cuyos lados tienen como longitudes números de Fibonacci consecutivos. Pide a los estudiantes que expandan el piso, utilizando el mismo criterio! Imagen de Wikipedia. O también, puedes dibujar una espiral como la de abajo. De hecho, la espiral se construye a partir del mismo piso de baldosas! Estos platos tienen como decoración unos cuadrados cuyos lados tienen longitudes tomadas de la secuencia de Fibonacci:  Photo by www.flickr.com/photos/darkemerald/5421772097 Por ejemplo, el plato en el medio podría ser de 21 cm por 21 cm (el cuadrado de color azul turquesa no se ve completamente), el cuadrado blanco en su interior podría ser de 13 cm × 13 cm, el cuadrado azul cielo podría ser de 8 cm × 8 cm, el negro podría ser 5 cm × 5 cm, y así sucesivamente. En la naturaleza, los números de Fibonacci se encuentran por ejemplo en la disposición de las semillas sobre la cabeza de ciertas flores. La siguiente imagen muestra una manzanilla amarilla y sus floretes, además espirales, algunas de color azul y otras de color agua. Si CUENTAS el número de espirales azules y luego el número de espirales color agua, obtendrás dos números de Fibonacci consecutivos! (¿Cuáles?)  Imagen por: Alvesgaspar y RDBury en Wikipedia => Continua leyendo |
2. Ejercicios para graficar rectasAhora puedes generar ejercicios en mi página para estos temas de álgebra (grados 7-9):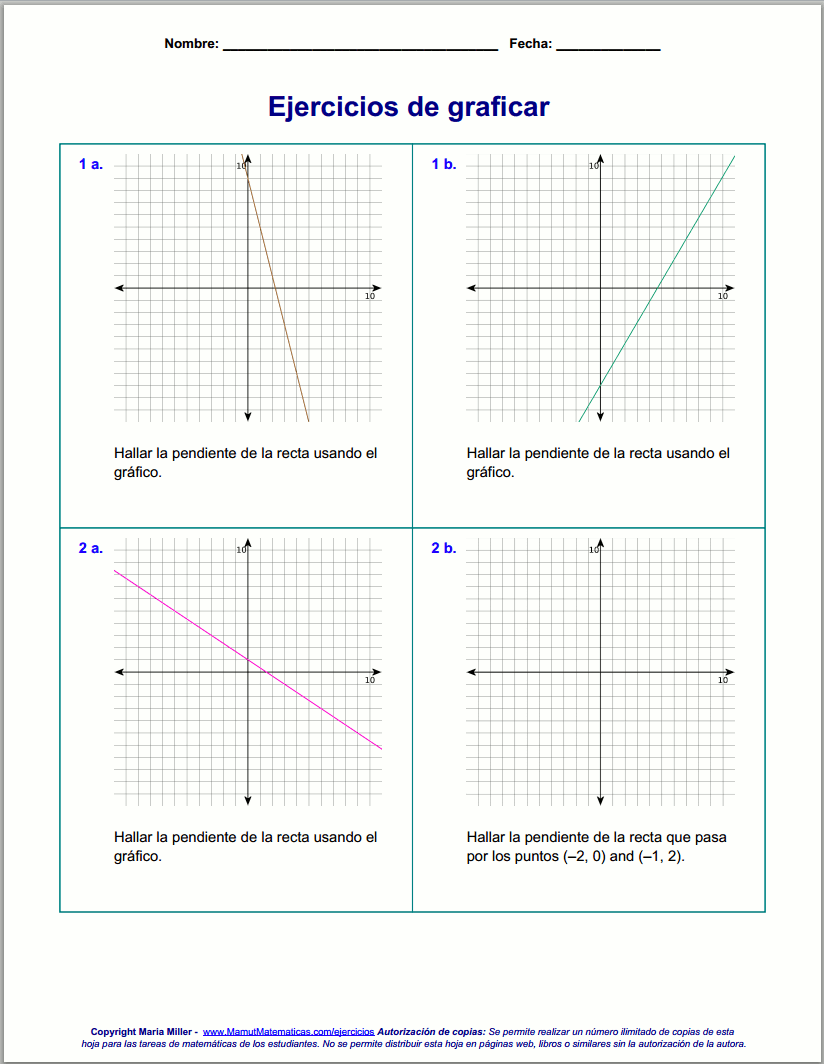
=> Ejercicios para graficar rectas |
Hasta luego,
Maria Miller
| Ejercicios gratuitos | Lecciones y juegos | |
| Libros Mamut | Archivo del boletín | |
--