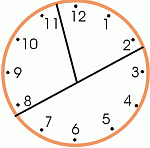
Boletín Mamut Matemáticas, Ed. 5; marzo 2008

¡Bienvenido a Boletín Mamut Matemáticas!

~ Abajo al final puede cambiar o cancelar su suscripción ~

En esta edición estudiamos ejemplos de cómo resolver problemas, le doy problemas para resolver a usted, y presento una idea de cómo los niños pueden hacer su propio diccionario de matemáticas.

En esta edición del boletin:

1. Ejemplo de resolver un problema: el problema de la cara del reloj

Este problema pertenece al quinto grado, y lo tomé de la colleción de problemás Word problems for kids por SchoolNet de Canada.

Quisiera usarlo para ilustrar el proceso de resolver problemas. Pero, antes de acudir a ver la solución, por favor, trate de resolverlo usted mismo.

Divide la cara del reloj en tres partes usando tres líneas asi que la suma de los números en las tres partes sea igual.

Primero necesitamos entender el problema. Se debe dibujar líneas en la cara del reloj. El problema no dice que las líneas deben terminar en el centro o cruzar por el centro. Parece que las líneas podrían pasar por muchas partes.

Para ayudar a un estudiante quien ni siquiera sabe cómo comenzar, simplemente pregútele dibujar algunas líneas en la cara del reloj. He aquí un ejemplo:

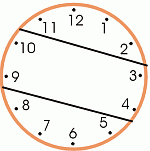
Claro que esto no es una solución porque no cumple con la condición que las sumás de los números en las tres partes sean iguales. Pero, le da un punto de comenzar. Tiene algunas líneas, así que puede pedir al estudiante que sume los números en las tres partes y notar que NO son iguales.

¿Cómo podemos hacer que las sumas sean iguales? Probando al azar tomaría mucho tiempo.

La CLAVE a este problema es que ya que las sumas en las tres partes son iguales, si sumas las sumas, tendrás la suma total de todos los números en la cara del reloj. Así, podemos hallar la suma parcial: primero calcular la suma total, y luego dividir por 3.

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = 78. 78 ÷ 3 = 26.

Entonces, la suma de los números en cada parte debe ser 26. Al resolver esta clave, hallando la solución a este problema es bastante facil.

Ahora necesitamos hallar los números en la cara del reloj que suman a 26. A base de probar, usted probablemente puede hallar el resultado pronto. Pero, también podemos pensar:

Consideramos primero el numero más grande en el reloj, el 12. ¿Qué otros números pueden acompañar al 12 para hacer 26? Probamos sumar varios de sus vecinos.

12 + 1 + 2 + 3 + 4 + 5 = 27, así que solo sumando los números del 1 y adelante no sirve.

Eso significa que necesitamos emparejar el 12 y el 11.

12 + 11 = 23. Falta tres. Luego... 12 + 11 + 1 + 2 le da 26. Es una de las partes que podemos separar usando una línea.

Luego, continuando desde los más grandes que quedan, 10 + 9 + 8 = 27. Es demasiado. Hace falta probar algo diferente.

Pero, dibujemos líneas a travez de la cara del reloj así que podemos unir el 10 con algunos números menores. Pronto verá que 10 + 9 + 3 + 4 = 26.

Los ultimos números que nos quedan son 5 + 6 + 7 + 8 = 26. Listo!

Ahora podemos probar si hay otra solución.

Note que solo se nos permite trazar dos líneas. No es posible hacerlo en muchas maneras diferentes. Puede dibujar dos líneas cruzando la cara del reloj, o acaso dibujar una línea a travez del reloj, y otra de la circunferencia a la primera línea, como en mi primer dibujo.

En la solución que hallamos, las dos partes consisten de números vecinos y la tercera parte (en el medio) no consiste de números vecinos. En cualquier caso, necesitamos usar algunos números vecinos para hacer las sumás de 26.

Cuando considera los números de 1 a 12 en la cara del reloj, los unicos números vecinos que suman hasta 26 son los que usamos: 12 + 11 + 1 + 2 y 5 + 6 + 7 + 8. Entonces, debemos usar por lo menos uno de esos conjuntos de números para una parte.

Si lo prueba, notará pronto que otras soluciones no son posibles.

Eso no se considera argumento totalmente rigoroso, juzgando por estandares matemáticos, pero es importante convencer a los estudiantes de que no hay otras soluciones. Convencer a otros de algo es el primer paso hacia la PRUEBA matemática.

2. Un problema para resolver: el problema del signo "+"

¿Cuántos signos de "+" se debería colocar entre los dígitos del número 987654321 y dónde los colocamos para alcanzar a la suma total de 99?

Este problema es para quinto grado tambien. Trate de resolverlo usted, o délo a sus hijos primero. Yo voy a tratar este problema en el boletin siguiente.

3. Un problema para resolver: la mesa que es más ancha y menos larga

El largo de una mesa rectangular es tres veces su ancho. Si fuera 3 m menos larga y 3 m más ancha, sería un cuadrado. ¿Cuáles son las dimensiones de la mesa rectangular?

Este problema es para sexto grado. Trate de resolverlo usted, o délo a sus hijos primero. Yo voy a tratar este problema en el boletin siguiente.

4. Su propio diccionario de matemáticas del niño

Esta es solo una idea que usted puede hacer con sus hijos/estudiantes, y es que ¡hagan su propio diccionario de matemáticas!

Simplemente necesita un cuaderno con hojas blancas. Cada vez que estudia un nuevo término o concepto, el niño completa una hoja nueva. Puede escribir el término, escribir una explanación breve o un ejemplo de alguna calculación que pertenece al concepto. Es recomendable dibujar una ilustración del concepto − ¡eso hace un diccionario muy lindo!

Hasta luego,
Maria Miller